\(\def\vec#1{\boldsymbol #1}\)

\(\def\pdif#1#2{\frac{\partial #1}{\partial #2}}\)

Система уравнений конвекции коллоидной суспензии

Рассмотрим горизонтальный слой коллоидной суспензии толщиной $h$ в однородном поле тяжести Земли $\vec g =-g\vec n_g ,\,\vec n_g=(0; 0;1)$. Слой ограничен сверху и снизу твердыми плоскостями, которые являются непроницаемыми и обладают идеальной теплопроводностью. Нижняя граница поддерживается при постоянной температуре $T_1$, а верхняя при температуре $T_2$, при этом $T_1>T_2$, что соответствует подогреву снизу. Ось $z$ направлена перпендикулярно слою, против силы тяжести. Оси $x$ и $y$ лежат в плоскости слоя (рис. 1 ). Слой считается бесконечным вдоль оси $y$.

Мы будем исходить из уравнения тепловой конвекции бинарной смеси в приближении Буссинеска [4]. В данном приближении полагается линейная зависимость плотности смеси от температуры и концентрации примеси:

\begin{equation} \rho = \hat{\rho} (1- \alpha T+\beta \delta C),\end{equation}

Здесь $\hat {\rho}$ -плотность смеси при средних значениях температуры и концентрации примеси. $ T,\delta C$- небольшие отклонения температуры и концентрации от средних значений ($\bar T,\, \bar C$), $\alpha,\beta$- коэффициенты теплового расширения смеси и концентрационного изменения плотности соответственно:

\begin{equation} \alpha=-\frac{1}{\rho} \frac{\partial \rho}{\partial T},\, \beta=\frac{1}{\rho} \frac{\partial \rho}{\partial C}.\end{equation}

В качестве $C$ выбрана концентрация тяжелой компоненты, поэтому увеличение концентрации примеси увеличивает плотность ($\beta>0$).В рамках приближения Буссинеска изменением плотности пренебрегается везде кроме слагаемого с подъемной силой, что позволяет считать жидкость несжимаемой.

Полная система уравнений, необходимая для решения данной задачи , содержит уравнение Навье-Стокса с учетом теплового и концентрационного изменения плотности, уравнение переноса тепла и уравнение неразрывности (для случая несжимаемой жидкости)[5]:

\begin{equation} \label{eq:main:v_r} \frac{\partial \vec v}{\partial t} +(\vec v\nabla)\vec v=-\frac{1}{\hat \rho}\nabla p +\nu\Delta \vec v+(\alpha T-\beta\delta C)\vec g,\end{equation}\begin{equation} \label{eq:main:t_r} \frac{\partial T}{\partial t}+(\vec v\nabla) T=\chi\Delta T,\end{equation}\begin{equation} \label{nr} {\rm div} \vec v=0,\end{equation}а также уравнение для переноса примеси, записанное с учетом термодиффузии и гравитационной седиментации:\begin{equation} \label{eq:main:C_r} \frac{\partial C}{\partial t}+(\vec v\nabla) C=D\left(\Delta C+S\Delta T+\frac{1}{l_{sed}}\frac{\partial C}{\partial z}\right).\end{equation}

Здесь используются следующие обозначения $\vec v$ -- скорость, $p$ -- отклонение давления от гидростатического, $C=\bar C+\delta C$ -- полная концентрация, $D$ -- коэффициент диффузии, $\nu$, $\chi$ -- коэффициенты кинематической вязкости и температуропроводности, соответственно, $S$ -- параметр термодиффузии, $l_{sed}$ -- длина седиментации, определяемая соотношением:\begin{equation}\label{eq:lsed} l_{sed}=\frac{k_b \bar T}{\delta\rho V g},\end{equation} где $\delta \rho=\rho_{{s}}-\rho_{{f}}$ -- разность плотностей твердой примеси и жидкости-носителя, $V$ -- объем частиц, $k_b$ -- постоянная Больцмана.

Граничными условиями на горизонтальных плоскостях являются условия прилипания для скорости (обращение скорости в ноль на твердых границах), постоянное значение температуры:\begin{equation}\label{eq:gr:v} \vec v(z=0)=\vec v(z=h)=0,\end{equation}\begin{equation} T(z=0)=T_1-\bar T=\theta/2,T(z=h)=T_2-\bar T=-\theta/2.\end{equation}

Для концентрации должно выполняться условие не проникания примеси через твердую границу, что требует обращение в ноль нормальной к границе составляющей потока вещества:\begin{equation} \label{eq:gr:c} \,\frac{\partial C}{\partial z}+S\frac{\partial T}{\partial z} +\frac{C}{l_{sed}}=0 \quad \mbox{при }\,\,z=0,h.\end{equation}

Система уравнений (\ref{eq:main:v_r})--(\ref{eq:main:C_r}) и граничных условий (\ref{eq:gr:v})--(\ref{eq:gr:c}) допускает решение, характеризующее механическое равновесие.

Поскольку все векторы ($\nabla T,\vec g, \, \nabla C$) перпендикулярны горизонтальным границам слоя, задача изотропна в плоскости слоя, поэтому можно искать решения, зависящие только от $x$.

Механическое равновесие

В состоянии механического равновесия распределения температуры и концентрации однородны вдоль оси $x$, и описываются уравнениями:\begin{equation}\label{t_r} \pdif{^2T}{z^2} =0,\end{equation}\begin{equation}\label{c_r} \pdif{^2C}{z^2}+\frac{1}{l_{sed}}\pdif{C}{z}+S \pdif{^2T}{z^2}=0,\end{equation}с граничными условиями:\begin{equation}\label{gr_tem_r} T(0)=\frac{\theta}{2},\,T(h)=-\frac{\theta}{2},\end{equation}\begin{equation}\label{eq:mr:c} \pdif{C}{z}+\frac{1}{l_{sed}}C+S \pdif{T}{z}=0 \quad\mbox{при} \quad z=0,h.\end{equation}

Решение уравнения для концентрации (\ref{c_r}) определено с точностью до константы. Однако в граничные условия концентрация входит в явном виде, что требует явного ее определения. Для этого необходимо учитывать условие постоянства средней концентрации:

\begin{equation}\label{con_post} \frac{1}{h}\int_0^h C dz=\bar{C}.\end{equation}

Данное условие говорит о том, что общая масса примеси остается неизменной.

Решение уравнения для температуры (\ref{t_r}) с учетом граничных условий (\ref{gr_tem_r}) имеет вид:\begin{equation}\label{term_rav} T=\theta\left(\frac{1}{2}-\frac{z}{h}\right).\end{equation}Подставляя данное решение в уравнение для концентрации (\ref{c_r}) и граничные условия (\ref{eq:mr:c}), получим:\begin{equation}\label{r_ct} \pdif{^2C}{z^2}+\frac{1}{l_{sed}}\pdif{C}{z}=0,\end{equation}\begin{equation}\label{r_ct_g} \pdif{C}{z}+\frac{1}{l_{sed}}C-\frac{S \theta}{h}=0\quad\mbox{при} \quad z=0,h.\end{equation}

Рассмотрим два предельных случая: отсутствия седиментации и отсутствия термодиффузии. При отсутствии седиментации, седиментационная длина стремится к бесконечности ($l_{sed}\to \infty$), тогда уравнение (\ref{r_ct}) и условие (\ref{r_ct_g}) примут вид:\begin{equation} \pdif{^2C}{z^2}=0.\end{equation}\begin{equation} \pdif{C}{z}=\frac{S \theta}{h}\quad\mbox{при} \quad z=0,h.\end{equation}Решение уравнения для концентрации с учетом условия (\ref{con_post}) запишется в виде:\begin{equation}\label{term_C} C_0=\bar{C}-S \theta\left(\frac{1}{2}-\frac{z}{h}\right).\end{equation}

Концентрация, как и температура, линейно зависит от вертикальной координаты. Градиент концентрации пропорционален коэффициенту Соре и приложенной разности температур. В зависимости от знака произведения $S\theta$ равновесное распределение концентрации может как стабилизировать ($S\theta<0$), так и дестабилизировать ($S\theta>0$) конвективную систему. Стабилизирующий профиль характеризуется градиентом концентрации, направленным вниз, при этом в нижних слоя жидкости концентрация тяжелой компоненты больше. Однако это не означает, что градиент плотности также направлен вниз, так как на неоднородность плотности так же влияет неоднородность нагрева.

При отсутствии термодиффузии (коэффициент Соре $S=0$) решением уравнения (\ref{r_ct}) с граничными условиями:\begin{equation} \pdif{C}{z}+\frac{1}{l_{sed}}C =0\quad \mbox{при}\quad z=0,1,\end{equation}является выражение:\begin{equation}\label{rav_c_T0} C_0=\frac{\bar{C}h}{l_{sed}}\frac{{e}^{(-z/l_{sed})}}{(1-{e}^{-h/l_{sed}})}.\end{equation}

В общем случае наличия седиментационного и термодиффузионного потоков решением уравнения (\ref{r_ct}) является выражение: \begin{equation}\label{rav_C_C0} C_0=C_*\exp\left(-\frac{z}{l_{sed}}\right)+\frac{S l_{sed}\theta}{h}.\end{equation}Сопоставляя выражения (\ref{rav_c_T0}), (\ref{term_C}), (\ref{rav_C_C0}) на первый взгляд кажется, что термодиффузия не может скомпенсировать гравитационное расслоение коллоида, однако это не так. Константа $C_*$, которая находится из условия постоянства средней концентрации (\ref{con_post}), зависит от температуры:

\begin{equation} \frac{1}{h}\int_0^h C dz=\frac{l_{sed}}{h}C_*\left[1-\exp(-h/l_{sed})\right]+\frac{S\theta l_{sed}}{h}=\bar{C},\end{equation}\begin{equation} C_*=\frac{\frac{\bar{C}h}{l_{sed}}-S \theta}{1-\exp(-z/l_{sed})}.\end{equation}Подставляя константу $C_*$ в уравнение (\ref{rav_C_C0}), находим равновесное распределение концентрации:\begin{equation}\label{con_TC} C_0=\left(\frac{\bar{C}h}{l_{sed}}-S \theta\right)\frac{{e}^{(-z/l_{sed})}}{1-{e}^{-h/l_{sed}}}+\frac{S\theta l_{sed}}{h}.\end{equation}

Таким образом, доказано, что общее решение (\ref{con_TC}) в предельных случаях дает либо чисто гравитационное, либо чисто термодиффузионное расслоение коллоидной суспензии.

В случае, когда седиментация и термодиффузия направлены в разные стороны ($S\theta>0$), распределение концентрации может быть однородным. Для нахождения этого условия приравняем концентрацию на верхней и нижней границе:\begin{multline} \left(\frac{\bar{C}h}{l_{sed}}-S \theta\right)\frac{1}{1-{e}^{-h/l_{sed}}}+\frac{S\theta l_{sed}}{h}=\\= \left(\frac{\bar{C}h}{l_{sed}}-S \theta\right)\frac{{e}^{(-h/l)}}{1-{e}^{-h/l_{sed}}}+\frac{S\theta l_{sed}}{h},\end{multline}откуда следует:\begin{equation} \frac{\bar{C}h}{l_{sed}}-S \theta=0,\end{equation}или:\begin{equation}\label{uslov_rav} \frac{\bar{C}h}{S \theta l_{sed}}=1.\end{equation}При выполнении условия (\ref{uslov_rav}) эффекты термодиффузии и осаждения примесных частиц под действием силы тяжести являются скомпенсированными. При этом распределение концентрации является однородным, не зависящим от координат. Условие (\ref{uslov_rav}) выполняется при некоторой критической температуре $\theta_R$:\begin{equation}\label{krit_term_rav} \theta_R=\frac{\bar{C}h}{Sl_{sed}}.\end{equation}Проверим правильность полученного результата, подставив данное значение температуры в уравнение для концентрации,\begin{equation}\label{con_kr_thet} C_0=\frac{S l_{sed}}{h} \frac{\bar{C}h}{l_{sed}S}=\bar{C}.\end{equation}Уравнение (\ref{con_kr_thet}) говорит о том, что при разнице температур между горизонтальными границами равной $\theta_R$ распределение концентрации является однородным во всем слое и равно средней концентрации.

Запишем уравнения (\ref{eq:main:v_r})--(\ref{eq:main:C_r}) в безразмерной форме, приняв в качестве единиц измерения следующие масштабы: расстояния -- толщину слоя $h$, времени -- $h^2/\chi $, скорости -- $\chi/h$, температуры -- $\theta =T_1-T_2$, концентрации -- $ \bar C h/l_{sed}$ и давления -- $\rho\chi^2/h^2$. При таком выборе единиц измерения безразмерная система уравнений примет вид:\begin{equation} \label{eq:main:v} \frac{\partial \vec v}{\partial t} +(\vec v\nabla)\vec v=-\nabla p +{ Pr}\Delta \vec v+{ Pr}({R}T-{ B}\delta C)\vec n_g,\end{equation}\begin{equation} \label{eq:main:t} \frac{\partial T}{\partial t}+(\vec v\nabla) T=\Delta T,\end{equation}\begin{equation} {\rm div} \vec v=0,\end{equation}\begin{equation} \label{eq:main:C} \frac{\partial C}{\partial t}+(\vec v\nabla) C={ Le}\left(\Delta C+\epsilon\frac{ R}{ B}\Delta T+\frac{1}{l}\frac{\partial C}{\partial l}\right),\end{equation}с граничными условиями:\begin{equation}\label{eq:main:v_gr} \vec v(z=0)=\vec v(z=1)=0,\end{equation}\begin{equation} T(z=0)=1/2,T(z=1)=-1/2,\end{equation}\begin{equation}\label{eq:main:C_gr} \,\frac{\partial C}{\partial z}+\epsilon\frac{R}{B}\frac{\partial T}{\partial z} +\frac{C}{l}=0 \quad\mbox{при }\,\,z=0,1.\end{equation}Уравнения в безразмерной форме содержат шесть безразмерных параметров: $Pr=\nu/\chi$ -- число Прандтля, $Le=D/\chi$ -- число Льюиса, $R=g\alpha \theta h^3/(\nu \chi)$ -- число Рэлея, $B=g\beta \bar C h^4/(\nu\chi l) $ -- число Больцмана, $l=l_{sed}/h$ -- безразмерная седиментационная длинна, $\epsilon =S \beta/\alpha $ -- параметр термодиффузии Соре.

В безразмерной форме распределение температуры (\ref{term_rav}) и концентрации (\ref{con_TC}) в равновесии примут вид:\begin{equation}\label{eq:T_0_rav_br} T_0=\frac{1}{2}\left(1-z\right)\end{equation}\begin{equation}\label{rav_con_br} C_0=\left(1-\epsilon \frac{R}{B}\right)\frac{e^{(-z/l)}}{1-e^{-1/l}}+\frac{l\epsilon R}{B},\end{equation}а условие однородного распределения концентрации (\ref{uslov_rav}) запишется как:\begin{equation}\label{eq:2.49} \frac{\epsilon R}{B}=1.\end{equation}

Конвекция при отрицательной термодиффузии

Сначала рассмотрим случай большой аномальной термодиффузии, пренебрегая гравитационным осаждением частиц. В данной задаче оба механизма (седиментация и термодиффузия) являются сонаправленными и седиментация не может качественно изменить характер течения. Уравнение (\ref{eq:main:v})--(\ref{eq:main:C}) без учета седиментации примут вид:\begin{equation}\label{eq:gl2:v} \pdif{\vec v}{t}+(\vec v \nabla) \vec v=-\nabla p+Pr\Delta \vec v+PrR(T- C)\vec n_g ,\end{equation}\begin{equation}\label{eq:gl2:t} \frac{\partial T}{\partial t}+(\vec v\nabla) T=\Delta T,\end{equation}\begin{equation} {\rm div} \vec v=0,\end{equation}\begin{equation}\label{eq:gl2:c} \frac{\partial C}{\partial t}+(\vec v\nabla) C=Le\left(\Delta C+\epsilon\Delta T\right).\end{equation}Здесь используются те же обозначения и масштабы измерения величин, что и в главе \ref{glava1}, за исключением того, что масштаб для концентрации выбран по-другому -- $\theta \alpha/\beta$.Отсутствие в уравнениях (\ref{eq:gl2:v})--(\ref{eq:gl2:c}) слагаемых пропорциональных полной концентрации позволяет рассматривать только ее отклонение от среднего значения. Здесь и далее мы будем вместо $\delta C$ использовать обозначение $C$. Отметим, что данные уравнения сохраняют зеркально-сдвиговую симметрию. Граничные условия, соответствующие твердым непроницаемым стенкам имеют вид:\begin{equation}\label{eq2:gr:1} x=0,1;\, \vec v=0;\, \,\pdif{C}{z}+\epsilon\pdif{T}{z}=0; \end{equation} \begin{equation}\label{eq2:gr:31} T(x=0,z)=T(x=1,z)=1-0.5z;\end{equation} \begin{equation}\label{eq2:gr:2} z=0,1;\, \vec v=0;\,\pdif{C}{x}+\epsilon\pdif{T}{x}=0; \end{equation} \begin{equation}\label{eq2:gr:3} T(x,z=0)=0.5;\,T(x,z=1)=-0.5.\end{equation}

Наличие аномальной термодиффузии приводит к тому, что концентрация тяжелой примеси становится больше в более нагретой жидкости. Существенным отличием от гравитационной седиментации является зависимость неоднородности распределения концентрации от температуры. При увеличении разности температур увеличивается и интенсивность термодиффузиионного разделения. Данный факт качественно отличает данную задачу от случая гравитационной седиментации, в которой интенсивность расслоения смеси является постоянной при изменении разности температур.

Уравнения (\ref{eq:gl2:v})--(\ref{eq:gl2:c}) с граничными условиями (\ref{eq2:gr:1})--(\ref{eq2:gr:3}) удовлетворяют условию отсутствия конвекции и допускают решение, при котором жидкость покоится. Распределение температуры и концентрации в состоянии механического равновесия обсуждалось в главе \ref{gl:meh_rav} и в данном случае выглядит так:\begin{equation}\label{eq:rav_c} T_0=0.5-z;C_0=-\epsilon(0.5-z).\end{equation}

Согласно работе[1], в которой рассматривалась конвекция коллоидной суспензии с параметром разделения Соре $\epsilon =-7.5$, средней концентрацией $\bar C=4\%$, состояние механического равновесия является устойчивым относительно бесконечно малых возмущений даже при очень больших значениях градиента температуры. Это, очевидно, связанно с устойчивой стратификацией плотности. При подстановке равновесного распределения температуры и концентрации в уравнение для плотности, записанное в безразмерной форме, мы получим равновесное распределение плотности: \begin{equation} \rho=1-\alpha \theta[T-C]=1-\alpha \theta[(0.5-z)(1+\epsilon)].\end{equation}Таким образом, вертикальный градиент плотности описывается уравнением:\begin{equation} \pdif{\rho}{z}=\alpha\theta(1+\epsilon).\end{equation}

Видно, что при $\epsilon=-1$ градиент плотности обращается в ноль. Это говорит о том, что плотность является постоянной во всей ячейке. При нагреве снизу ($\theta>0$) и $\epsilon<-1$ градиент плотности направлен вниз, что соответствует устойчивой вертикальной стратификации.

В коллоидных суспензиях при отсутствии начального градиента концентрации возможно существование устойчивых течений. Расчеты показали, что возникновение существенных неоднородностей концентрации происходит за диффузионное время. Для коллоидных жидкостей отношение характерного теплового ($\tau_T$) и диффузионного ($\tau_D$) времен $\tau_D/\tau_T =\chi/D\sim 10^4 $. В связи с этим начальные течения, на временах много меньше диффузионного времени, схожи с течениями однородной жидкости. Однако, возникающая впоследствии неоднородность концентрации изменяет картину течения, приводит к возникновению волновых режимов. Данные течения являются строго нелинейными. Поэтому применение линейной теории устойчивости для анализа порога возникновения таких течений становится невозможным. Для получения информации о возможных течениях и границах их устойчивости необходимо решать полную нелинейную систему (\ref{eq:gl2:v})--(\ref{eq:gl2:c}) с граничными условиями ( \ref{eq2:gr:1})--(\ref {eq2:gr:3}).

Для коллоидных жидкостей характерны малые значения коэффициента диффузии. Например, в случае коллоидной суспензии Hyflon MFA $D=1.30\cdot 10^{-7}\, \mbox{см}^2/\mbox{с}$ [1]. Таким образом, характерное время, за которое протекают диффузионные процессы $\tau_D=h^2/\pi^2D$, очень большое. Для ячейки высотой $h=0.29$ см, которая использовалась в экспериментальной работе [1]$\tau_D=h^2/\pi^2D\approx 6.47 \cdot 10^4 c\approx 18$ часов. Однако, при установившемся конвективном течении, диффузионные процессы протекают не во всей ячейке, а только в тонких слоях на границе конвективных валов. Переходные процессы, возникающие при изменении внешних параметров, протекают за меньшее время, но это время все же остается довольно большим в сравнении с характерными гидродинамическим и тепловым временами.Поэтому переходный процесс также требует изучения, как и стационарные течения.

Значения безразмерных параметров системы (\ref{eq:gl2:v})--(\ref{eq:gl2:c}) в численном моделировании были выбраны для соответствия реальной коллоидной суспензии Hyflon MFA [1]:\begin{equation} Le=8.84\times10^{-5},\end{equation}\begin{equation} \epsilon=-7.5,\end{equation}\begin{equation} Pr=6.0.\end{equation}

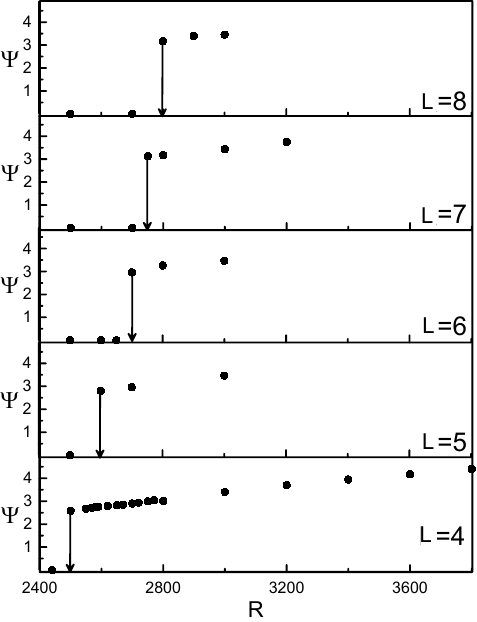
Для основных расчетов была выбрана ячейка с соотношением сторон ${\rm L}=l_x/l_z=4.14$ и сетка 342x82. Для проверки результатов сделаны несколько расчетов на сетке 682x178, которые подтверждают результаты, полученные на сетке 342x82. Кроме этого были произведены вычисления и для других соотношений сторон: ${\rm L}=3,4,5,6,8$.

Начальная стадия эволюции. Формирование бегущей волны

Обсудим результаты численного моделирования.Конвекция в данной задаче сильно зависит от начальных условий. Если в качестве начальных условий задается полностью установившееся термодиффузионное распределение концентрации (\ref{eq:rav_c}), то все возмущения затухают. Данный результат согласуется с результатами экспериментальных работ [1].

При однородном начальном распределении концентрации возможно возникновение устойчивых конвективных течений. На начальной стадии конвекция представляет течение однородной жидкости, на которое оказывает влияние лишь градиент температуры. Наблюдается стационарная однородная конвекция. Через некоторое время стационарное течение теряет устойчивость, и образуется бегущая волна. При уменьшении интенсивности нагрева бегущая волна со временем так же может потерять устойчивость, при этом течение полностью затухает.

Несмотря на конвективное перемешивание, в первоначально однородной жидкости за счет термодиффузии возникает градиент концентрации. Концентрация тяжелой примеси увеличивается на нижней границе (уменьшается на верхней). Интенсивность стационарной конвекции при этом уменьшается, так как приводит к потоку тяжелых частиц в более нагретые области. При некоторой неоднородности концентрации стационарное течение становится неустойчивым, и образуется бегущая волна. При расчетах наблюдаются волны бегущие вправо и влево (при решении уравнения для функции тока методом рядов Фурье). В силу симметрии задачи направление движения волн вправо и влево являются эквивалентными. Все дальнейшие результаты относятся к волнам бегущим вправо.

Отметим, что переходный процесс от стационарного течения к бегущей волне занимает менее 10 единиц безразмерного времени, в то время как стационарный режим существует порядка 800 единиц, для значения числа Рэлея $R=3.6\cdot 10^3$. Время существования режима стационарной конвекции уменьшается при уменьшении числа Рэлея (уменьшении интенсивности конвекции), для $R=2.5\cdot 10^3$ составляет порядка 170 единиц.

Диффузионные процессы не успевают сгладить разность концентраций внутри конвективного вихря за время его существования. Примесь закручивается в спираль, при этом в центре конвективного вихря наблюдается превышение концентрации над средним значением. Так как диффузия мала, неоднородности концентрации сглаживаются очень медленно, и тонкая спиральная структура существует внутри вихря вплоть до его разрушения на правой границе ячейки. Существование скопления частиц в центре вихря обусловлено тем, что в ядре вихря вертикальная скорость равна нулю. Таим образом, конвективное перемешивание в центре вихря практически отсутствует и, в силу малости диффузии, неоднородность концентрации может существовать длительное время, больше времени жизни вихря при его движении внутри ячейки.

Устойчивое течение существуют при $R>R_S=2.45\cdot 10^3$. Ниже $R_S$ также можно наблюдать бегущие волны, но с течением времени, после переходного процесса, они затухают.

Вообще говоря, медленные переходные процессы создают дополнительную трудность в анализе режима бегущих волн. Помимо больших затрат машинного времени возникает проблема определения выхода течения на конечное состояние, так как все характеристики течения меняются довольно медленно на фоне колебательных процессов, но на больших временах могут привести к значительному изменению.

Бифуркационная диаграмма

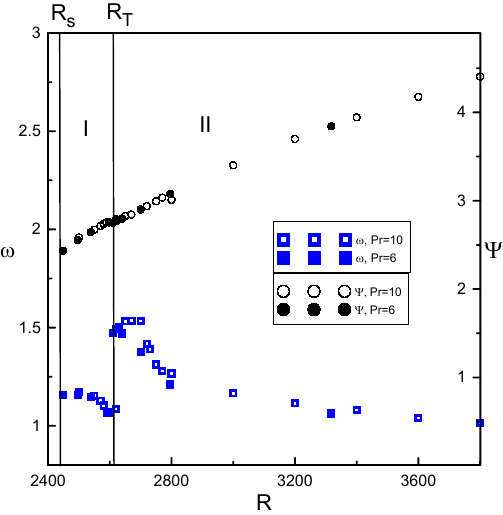
В результате исследования было обнаружено два устойчивых режима конвекции, при этом они непрерывно переходят друг в друга при рассмотрении зависимости максимального значения функции тока от числа Рэлея. Однако при спектральном Фурье-анализе обнаруживается их качественное различие.

Бифуркационная диаграмма конвективных режимов приведена на \mbox{рис. 2 }. Данная диаграмма рассчитана при значении числа Льюиса $Le=8.84 \times 10^{-5}$ и двух значений числа Прантдля $Pr= 6$ и $Pr=10$. На ней отображены зависимости максимального значения функции тока $\Psi_{max}$ и основной частоты бегущей волны (имеющей максимальную амплитуду в спектре Фурье) $\omega_m$ от числа $R$. Наблюдаются две бифуркации. Значения числа Рэлея, при которых происходит смена конвективного режима, обозначены $R_S$ и $R_T$.

Как уже было отмечено, устойчивые течения существуют при $R>R_S=2.45\cdot 10^3$, при этом течение возникает жестким образом. При числах Рэлея от $R_S=2.45 \cdot 10^3$ до $R_T=2.62\cdot 10^3$ существует режим бегущих волн с множеством кратных частот. На бифуркационной диаграмме он обозначен (I). При $R>R_T$ наблюдается либо монохроматический режим, либо режим с тремя частотами, он обозначен (II). Различие данных режимов видно при рассмотрении спектров Фурье.

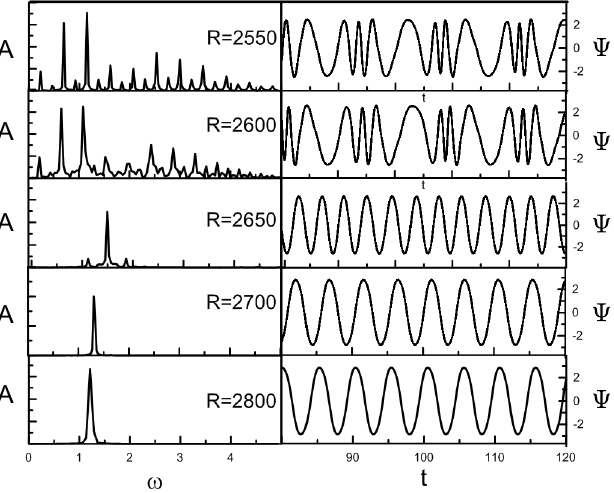
На рис. 3 приведены временные Фурье-спектры и поведение функции тока в фиксированной точке $\Psi_{loc}=\Psi(x=3/2,z=1/2)$ для обоих режимов конвекции. Так как в конвективном режиме I наблюдается множество временных частот, на бифуркационной диаграмме отображена частота имеющая наибольшую амплитуду. Расчеты показывают, что значения критических чисел Рэлея $R_S,\,R_T$, при которых происходят бифуркации, не зависят от числа Прандтля.

При больших числах $R$, в спектре Фурье наблюдается одна частота, которая увеличивается с уменьшением числа $R$. При $R<2.67\cdot 10^3$ появляются две дополнительные частоты (рис. 3 ), причем дополнительные частоты имеют одинаковую амплитуду и их частоты отличаются от основной частоты на величину $\pm\delta \approx \omega_m/4$ ($\omega_m$ -- основная частота). Бегущая волна становится модулированной. При этом $\omega_m$ начинает уменьшаться с уменьшением $R$.

В режиме I наблюдается большой спектр частот, однако все частоты спектра являются кратными первой частоте , то есть $\omega_n=n\omega_1$, где $n$ целое число. Частоты c нечетными $n$ имеют большую амплитуду.

Значение $R_S$ является границей устойчивости начального однородного распределения концентрации как для бесконечно малых возмущений, так и для возмущений конечной амплитуды. То есть при $R>R_S$ любое малое возмущение со временем развивается в устойчивое течение. С другой стороны любое течение при $R<R_S$ затухает.

При анализе частотных спектров хорошо видно качественное различие данных режимов. Однако при этом интегральные характеристики течений, такие как число Нюссельта ($Nu$) или максимальное значение функции тока, различаются незначительно при смене конвективного режима.

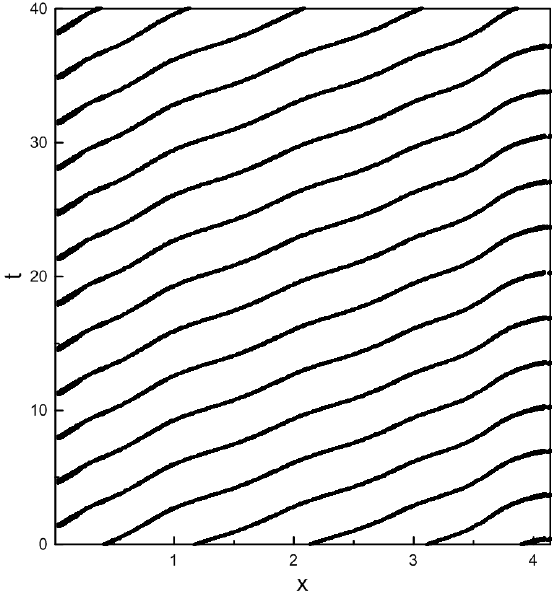
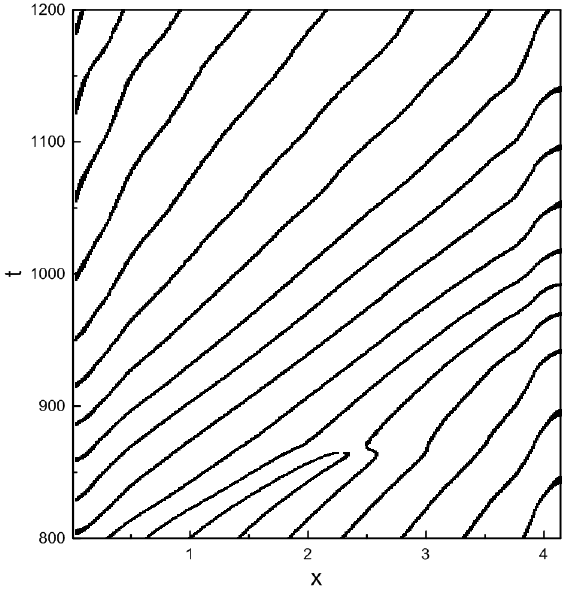
На характеристической плоскости, которая показывает координаты центров вихрей (узлов вертикальной скорости) со временем, мы видим, что в режиме II (рис. 4 ) все узлы движутся приблизительно с одинаковой скоростью, при этом наблюдается небольшая модуляция. Также можно видеть, что в определенные моменты времени число вихрей различно, от 3 до 5.

В режиме I (рис. \ref{spf2}) можно условно выделить две группы вихрей. Существуют вихри, которые пробегают через всю ячейку, практически не меняя своей скорости, например, вихри, зарождающиеся при $x=0$, в момент вермени $t=5$ или $t=20$. С другой стороны появляются такие вихри, которые существенно меняют фазовую скорость за время своей жизни, причем, в середине слоя они бегут медленнее. Данный факт свидетельствует об усложнении течения при понижении подогрева, что кажется противоречивым лишь на первый взгляд. Усложнение течения может быть связанно с тем, что при понижении числа $R$ частота волны, а следовательно и ее фазовая скорость, увеличиваются. При этом увеличивается скорость с которой концентрационная волна набегает на стенку. Состояние с большой частотой может становиться неустойчивым, и оно переходит в немонохромный режим с меньшими частотами. Также это может быть связано с тем, что при меньших числах $R$ уменьшается интенсивность течения. Это приводит к уменьшению интенсивности перемешивания коллоида, и неоднородность распределения концентрации увеличивается.Похожее поведение системы было обнаружено в ходе экспериментов по изучению конвекции в горизонтальном слое [6].

При понижении интенсивности нагрева $R<R_S$ все течения затухают. Бегущая волна продолжает существовать в течении некоторого времени. При этом разность концентраций растет. Увеличивается частота бегущей волны, ее структура начинает разрушаться. Время затухания возмущений при числе Рэлея немного меньшем $R_S$ является достаточно большим и резко уменьшается с уменьшением $R$. Так для числа $R=2.4\cdot 10^3$ время затухания бегущей волны $\tau= 140$, для $R=2.3\cdot 10^3$ -- $\tau=71$ и для $R=2.0\cdot 10^3-\, \tau<10$.

Анимация течения привелена на видео 5 6

Влияние длины ячейки

Так как бегущие волны распространяются вдоль оси $x$, длина полости вдоль данной оси влияет не только на структуру течения, но и на критическое число Рэлея.

На рис. 7 приведены бифуркационные диаграммы для различных значений аспектного соотношения ${\rm L}=l_x/l_z$. При расчетах пространственный шаг сетки сохранялся, то есть при увеличении длины ячейки увеличивалось и число узлов расчетной сетки.Видно, что при увеличении длины ячейки порог устойчивости механического равновесия смещается в сторону больших значений числа $R$. Минимальное значение частоты $\omega$ достигается при длине ячейки порядка 5 единиц. При ${\rm L}\leq 2$ бегущая волна не образуется. Критическое число Рэлея при ${\rm L}=8$ составляет $R\approx 2.8\cdot 10^3$. Согласно результатам экспериментов, описанных в [1] порог конвективной устойчивости в плоской кювете с соотношением высоты к длине $8.14$ составляет $R_c\approx 3.4\cdot 10^3$, что выше результата, полученного путем нашего численного моделирования на $17\%$.

В длинных полостях проявляются качественно новые эффекты, которые не наблюдаются в коротких ячейках. На характеристической плоскости (рис. 8 ), построенной для ячейки с ${\rm L}=8$, наблюдаются дефекты, при которых два вихря сливаются и уничтожают друг друга. Кроме этого, поведение вихрей становится более сложным. При сравнении характеристических плоскостей для ячейки с длинной ${\rm L}=4$ (рис. 4 ) и ${\rm L}=8$ (рис. 8 ) видны существенные отличия. Так в длинных ячейках не удается разделить волны на две группы, ввиду более сложного поведения каждого вихря.

В качестве предельного случая бесконечно длинного канала, мы можем рассматривать часть канала с периодическими граничными условиями на вертикальных границах. Мы рассматривали ячейки длинной ${\rm L}=2$ и ${\rm L}=4$. Для данной геометрии не удалось получить устойчивых течений в области $2.4\cdot 10^3<R<6\cdot 10^3$. Этот факт подтверждает выводы о том, что причиной возникновения волны является взаимодействие течения с вертикальной стенкой.

Переходные процессы

В длинных ячейках при понижении числа Рэлея ниже критического значения $R_s$ наблюдаются длительные переходные процессы, в которых проявляются разнообразные конвективные режимы: бегущие волны, локализованные бегущие волны, стоячие волны. Анимация течения приведена на 9

Локализованная бегущая волна существует в области длинной порядка 4 единиц, что соответствует удвоенной длине бегущей волны. При этом образование и разрушение конвективных вихрей происходит вдали от границ полости. Вне области существования локализованной бегущей волны жидкость практически неподвижна. Границы области течения остаются неподвижными некоторое время. Режим локализованной бегущей волны является неустойчивым. Развитие течения может привести, как к разрушению локализованного состояния с образованием стоячей волны, так и к развитию бегущей волны во всем слое.

В процессе эволюции течения, направление движения бегущей волны может изменяться. Так же возможно существование таких течений, при которых две бегущие волны разбегаются в разные стороны, от середины ячейки к краям.

Работа выполнена при поддержке грантов: 14-01-31299 мол_а, 14-01-96027.