\(\def\vec#1{\boldsymbol #1}\)\(\def\pdif#1#2{\frac{\partial #1}{\partial #2}}\)

Введение

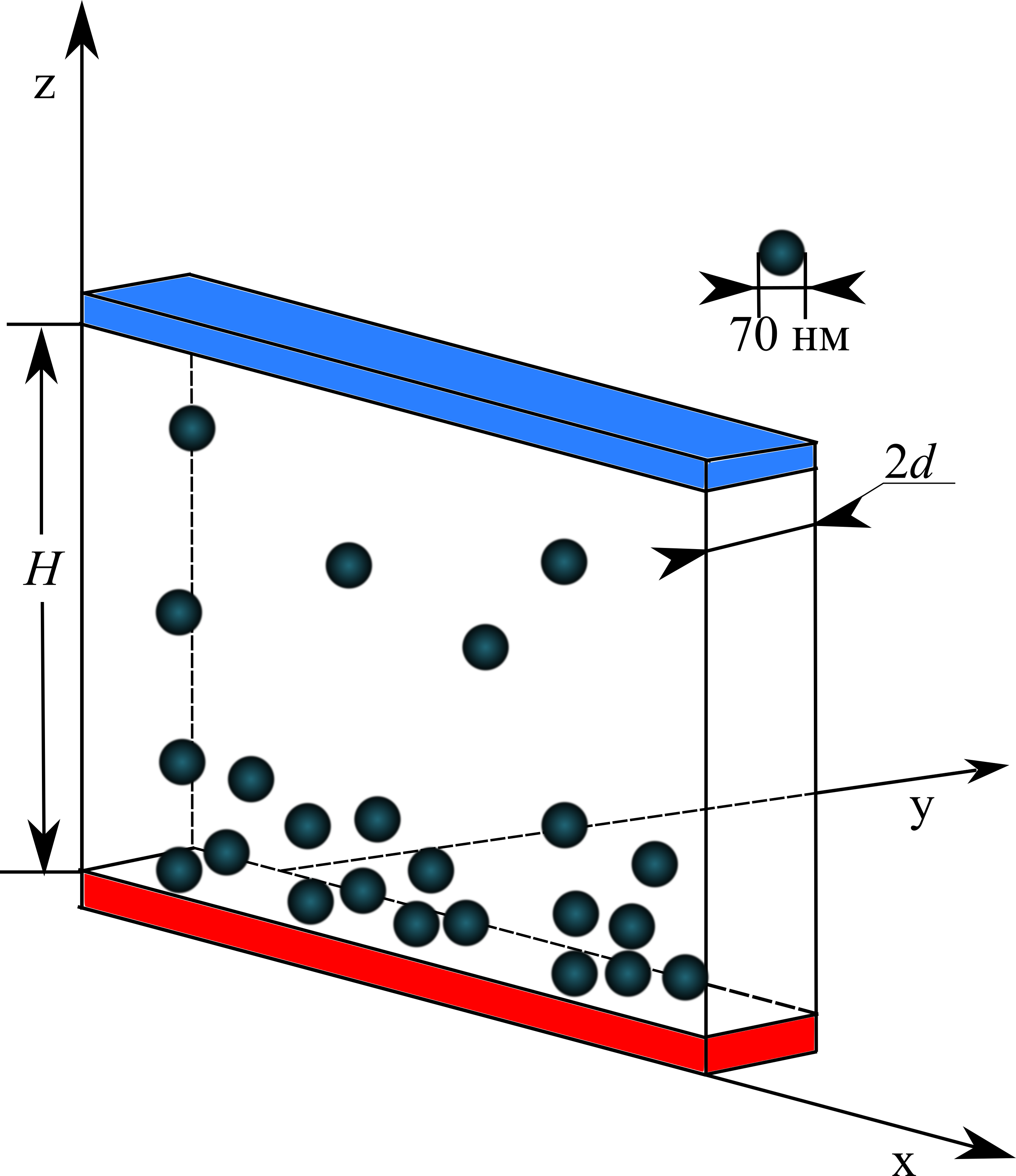
Рассмотрим горизонтально ориентированный бесконечный плоский канал, ширина $d$ которого много меньше его высоты $H$ , $H/d=20:2$ (рис. 1 ). Канал данной геометрии традиционно называют ячейкой Хеле-Шоу.

Канал заполнен коллоидной суспензией и находится в поле тяжести $\vec g$. На горизонтальных плоскостях поддерживаются разные температуры, создавая постоянный градиент, направленный вниз. Неоднородность концентрации наночастиц в покоящейся коллоидной суспензии создается двумя механизмами: гравитационной стратификацией коллоида, а также нормальным эффектом термодиффузии Соре (тяжелые частицы мигрируют к холодной границе).

Описание конвекции коллоидной суспензии проводится на базе уравнений конвекции бинарной смеси в приближении Буссинеска, в котором предполагается линейная зависимость плотности от температуры и концентрации:\begin{equation} \rho = \rho_0(1-\alpha T-\beta T)\end{equation}

Основные уравнения

Широкие грани ячейки являются являются твердыми и теплоизолированными. \begin{equation} v=0; \pdif{T}{y}=0; \pdif{C}{y}=0. \end{equation}

Распределение температуры и концентрации вдоль оси $y$ считается постоянной: \begin{equation}T(x,y,z,t)= T_0(z)+\theta(x,z,t)\end{equation}\begin{equation}C(x,y,z,t)=C(x,z,t)\end{equation}Полная система уравнений в приближении Хеле-Шоу в терминах функции тока и температуры имеет вид:\begin{equation}\pdif{\phi}{t}+\frac{8}{3\pi} \left(\pdif{\Psi}{z}\pdif{\phi}{x}-\pdif{\Psi}{x}\pdif{\phi}{z}\right)={Pr}\Delta_1 \phi -{Pr}\frac{\pi^2}{4}\phi-\frac{4}{\pi}{Pr} \left(R\pdif{\theta}{x}-{B} \pdif{C}{x}\right)\end{equation}\begin{equation}\pdif{\theta}{t}+\frac{2}{\pi}\left(\pdif{\Psi}{z}\pdif{\theta}{x}-\pdif{\Psi}{x}\pdif{\theta}{z}\right)=\Delta_1 \theta -\frac{2}{\pi}\pdif{\Psi}{x}\end{equation}\begin{equation}\pdif{C}{t}+\frac{2}{\pi}\left(\pdif{\Psi}{z}\pdif{C}{x}-\pdif{\Psi}{x}\pdif{C}{z}\right)=Le\nabla\left( \nabla C+\frac{1}{l}C\vec{n_g}+\frac{\varepsilon R}{B}C\nabla \left(T_0+\theta\right)\right) \end{equation}

Задача содержит следующие безразмерные параметры

\begin{eqnarray*}R = \frac{g\alpha h^3 \theta}{\chi\nu}; && B = \frac{g\beta\bar C h^3}{\chi\nu}\frac{h}{l_{sed}};\\Le = \frac{D}{\chi} ; & & Pr = \frac{\nu}{\chi} ; \\l = \frac{h}{l_{sed}} ; & & l_{sed} =\frac{k_b T}{\Delta \rho V g} ;\\ \psi =\varepsilon \hat C = S_T\frac{\alpha}{\beta} .&& \end{eqnarray*} Начальные распределения концетрации задавалось уравнением:\begin{equation*} C_0= H\gamma \frac{e^{\gamma z/l}}{e^{\gamma H/l}-1}; \gamma=\frac{\varepsilon R}{B}-1\end{equation*}

при расчетах использовались следующие безразмерные параметры:\begin{eqnarray*} Le &=& 5 \times 10^{-4};\\ P&=&48;\\ \psi&=& 8.8.\end{eqnarray*}

Задача решалась методами конечных разностей. Для функций вихря и температуры использовались явные методы с центральными разностями по пространственной координате. Уравнение Пуассона для функции тока решалось прямым методом, основанным на разложении функции тока в ряд Фурье. Для уравнения концентрации использовалась явная схема контрольного объема [2]. Использование данной схемы, а также консервативная форма записи уравнений переноса позволяет добиться выполнения закона сохранения массы. Основные расчеты были произведены с использование сетки содержащей 257X65 узлов. Явные схемы были выбраны, так как использование не явных алгоритмов, основанных на методе прогонки, становиться не возможным ввиду условий Неймана для концентрации на всей границе [2].

Результат

Наличие примеси существенно изменяет картину течений жидкости в ячейке Хеле-Шоу.В отсутствии термодиффузии возникновение течения происходит жестким образом, при этом в близи пора существования течения наблюдаются колебательный режим конвекции типа бегущих волн, обнаруженный ранее при конвекции коллоидной жидкости в плоском слое ( 2 ).

При числе $B=0.16$ состояние механического равновесия остается устойчивым относительно малых возмущений при числах Релея $R<0.47$, что соответствует приведенному числе $R*=R/R_0=1.34$, где $R_0$ – порог возникновения течения в однородно жидкости. При больших числах Релея интенсивное конвективное течение полностью примешивает примеси. Внутренне механизмы формирования неоднородностей, в виду малых значений коэффициентов переноса (малых числе Льюиса), не способны создавать значимые неоднородности концентрации.

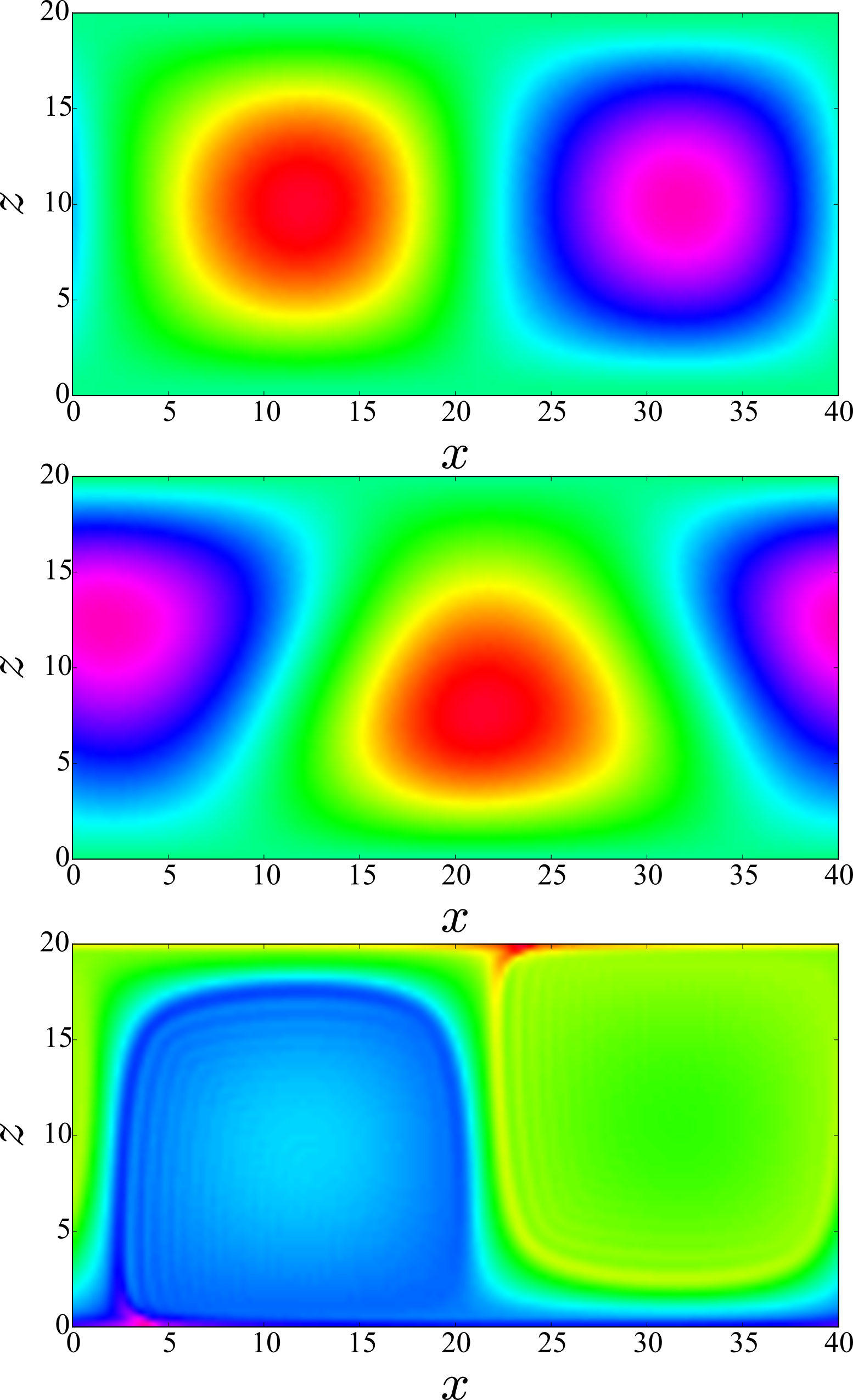
При понижении интенсивности нагрева скорость течения уменьшается, а вместе с ним и конвективное перемешивание примеси, что приводит к формированию заметных неоднородностей концентрации. Вблизи порога существования течения наблюдается режим бегущих волн, изолинии которого приведены на рисунке 3 .

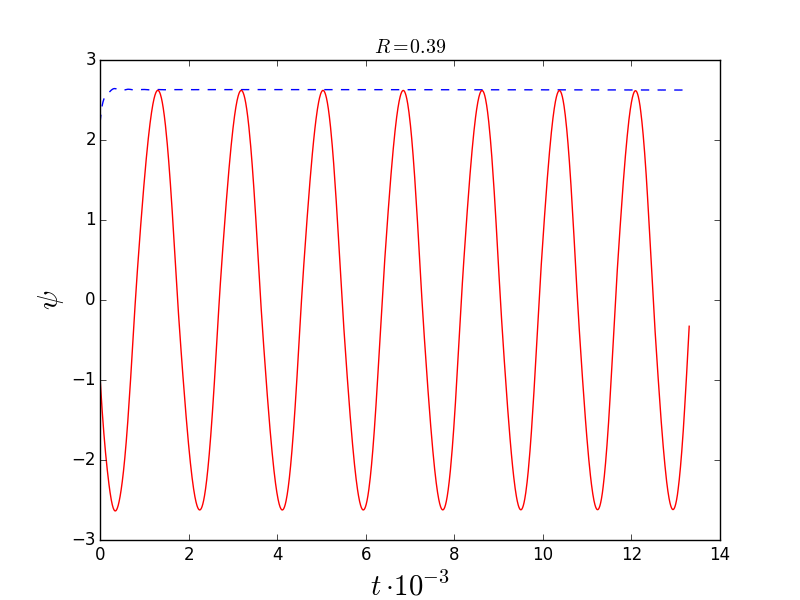
Как и в случае бесконечного плоского слоя частота бегущей волны увеличивается при уменьшении параметра Релея[3,4]. Поведение функции тока в фиксированной точке в центре слоя приведены на 4 .

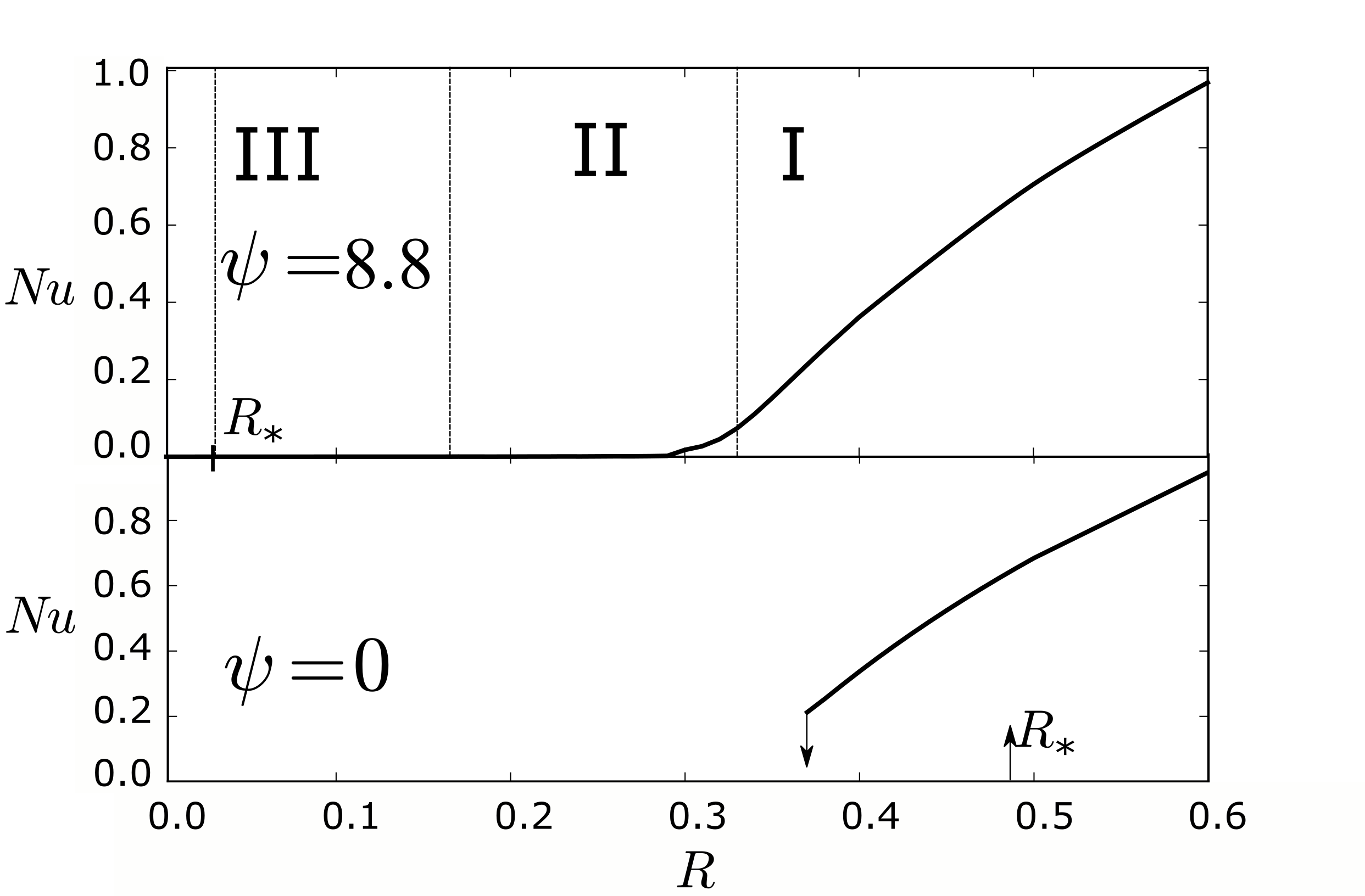
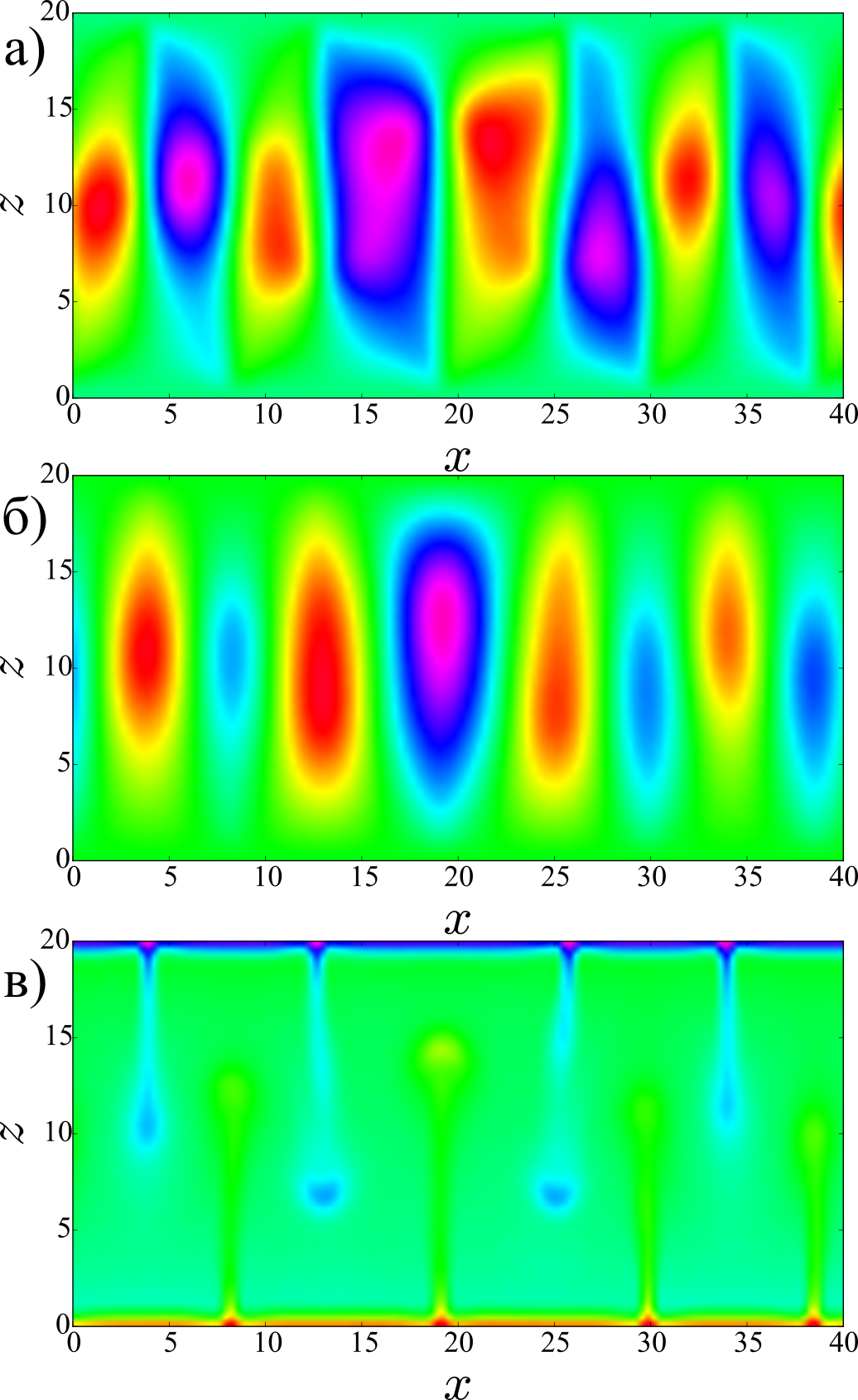
При положительной термодиффузии было обнаружено три конвективных режима ( рис. 2 ). Наличие положительно термодиффузии приводит не только к смещению порога устойчивости, но также и смене характера бифуркации.

При больших числах Релея (область I 2 .) существует режим стационарной однородной конвекции, по внешнему виду такой же, как и при отсудив термодиффузии.

В области знаний параметров обозначенных II на рис 2 наблюдается сложных хаотический режим концепции. В данном режиме наблюдаются мелкомасштабные пальцеобразные конвективные существуют на фоне крупномасштабного колебательного течений. Анимация полей концентрации приведена на видео 6

Расчёты, проводимые на довольно больших временах (порядка $10^5$ тепловых единиц времени), показали устойчивости данного режима.

При малых числах Релея (область III рис 2 .) обнаружен слабый колебательный режим. В данном режиме пальцевидные структуры являются упорядоченными в пространстве (рис. 7 ).

Однако данный режим является колебательным. Ввиду малой интенсивности течения тепловой поток через ячейку является малым.

Переходный режим

При больших числах Релея наблюдается сложный переходный режим течения.В изначально стратифицированной жидкости при приложении градиента температуры на фоне равновесного профиля концентрации появляются пальцеобразные структуры с волновым числом порядка k=.

Неравномерное появление структур вдоль оси x связано с видом началах возмущений для функции тока, которые представляют собой два слабых вихря разной закрутки. Асимметрия верхнего и нижнего течения связана с зависимостью параметра термодиффузии от концентрации. В верхних слоях концентрация примеси меньше, следовательно, меньше и термодиффузионный поток. Далее начинает образовываться стоячая волна, при этом пальцы концентрации продолжат всплывать. Течение представляет собой суперпозицию мелкомасштабных конвективных факелов и крупномасштабной стоячей волны. Затем она, стоячая волна, разрушается и образуется волна бегущая. Бегущая волна существует в течении длительного времени, после чего движение вихрей вдоль горизонтальной оси останавливается и наблюдается режим стационарной однородной конвекции.

Работа выполнена при поддержке грантов: 14-01-31299 мол_а, 14-01-96027.