\(\def\vec#1{\boldsymbol #1}\)

\(\def\pdif#1#2{\frac{\partial #1}{\partial #2}}\)

Введение

При рассмотрен коллоидных смесей зачастую рассматриваются каналы, высота которых намного меньше седиментационной длины. При этом распределение примеси по высоте, обусловленное гравитационным разделение, является практически линейный.

Малые частицы погруженные в жидкость поддерживаются во взвешенном состоянии благодаря тепловому движению. Однако в поле силы тяжести распределение концентрации по высоте является неоднородным [1,2], что оказывает существенное влияние на конвективные течения [3]. Интенсивность гравитационного разделения определяется из соотношения тепловой энергии движения молекул и энергии гравитационного поля[4]:

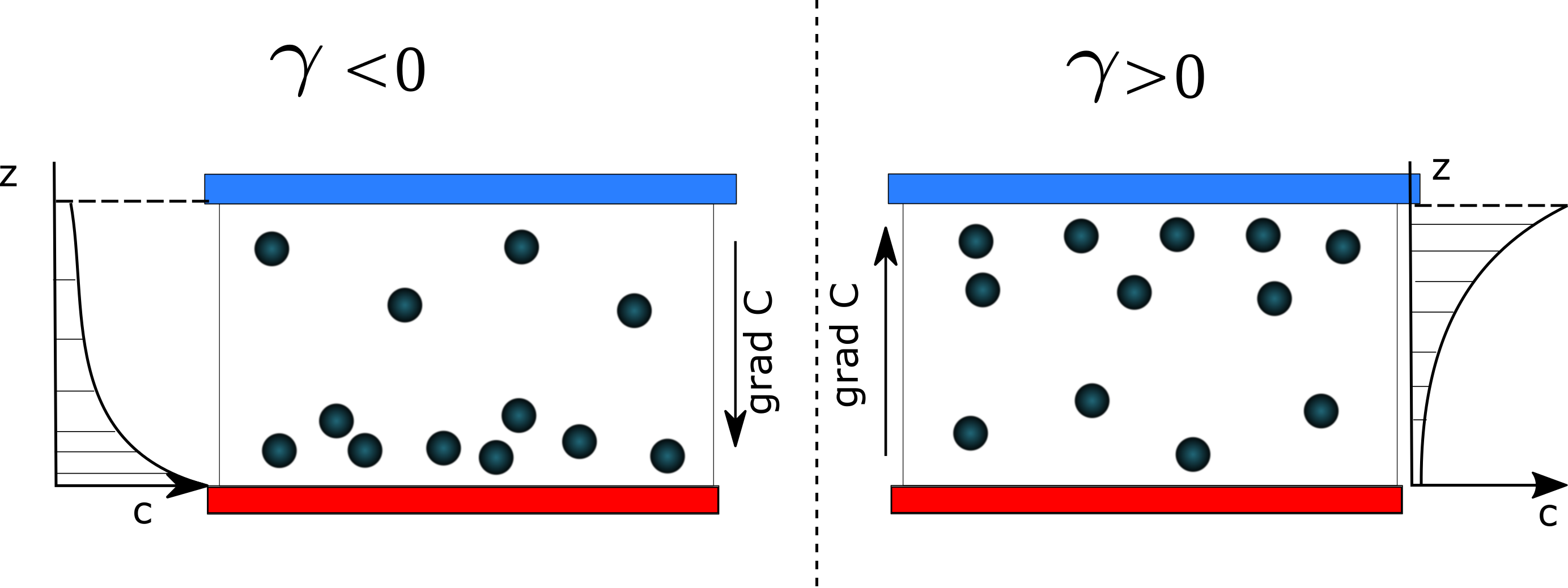
\begin{equation} l=\frac{k_bT}{\delta \rho Vg} \end{equation}$\delta \rho=\rho_s -\rho_f$ -- разность плотности жидкости носителя и частиц примеси, $V$ --объем частиц, $g$ -- ускорение свободного падения, $k_b$ --постоянная Больцмана, $T$ -- абсолютная температура, $l$ -- высота, на которой концентрация уменьшается в $e$ раз [4]. В неоднородно нагретом коллоиде появляться дополнительный механизм формирования неоднородности плотности за счет термодиффузионного разделения [5,6].При изучении конвективных течений коллоидов необходимо учитывать оба механизма. [5,7]Если макроскопическое движение жидкости отсутствует, то распределение коцнетрации описывается ворожением: \begin{equation} C=\frac{\gamma \exp\left( \gamma z\right)}{1- \exp \left(\gamma h\right)}; \gamma= -\frac{1}{l}+S_T\delta T \end{equation}где $\delta T$ -- приложенная разность температур, $S_T$ -- коэффициент Соре, $h$ -- высота слоя. Таким образом, в случае если $\gamma<0$ концентрация тяжелых частиц выше в нижних слоях, а при $\gamma>0$ концентарция наночастиц будет больше в верхних слоях ячейки (см рис. 1 ).

Если средня концентрация примеси остается малой зависимостью вязкости и температуропроводности от концентрации можно пренебречь, а плотности считается линейной функцией концентрации, при этом приближении Буссинеска остается справедливым при условии [8]:\begin{equation}\alpha \delta T<<1;\, \beta\delta C<<1\end{equation} где $\alpha$, $\beta$ -- коэффициенты теплового и концентрационного расширения. $\delta T,\, \delta C$ -- характерная разность температуры и концентрации.

Уравнения

Для математического описания конвективных течений будем исходить из уравнений тепловой конвекции в приближении Буссиненска[8]в котором полагается линейная зависимость плотности от температуры и коцнетрации:\begin{equation} \rho =\rho_0(1-\beta_T \delta T +\beta_C \delta C)\end{equation}

Полная система уравнений конвекции наножидкости будет включать в себя уравнения эволюции скорости, температуры и коцнетрации:\begin{equation}\pdif{v}{t} +v \nabla v= -\frac{1}{\rho} \nabla p + \nu \Delta v + g\vec n_g\left( \beta_T T+ \beta_C C \right),\label{eq:in:v}\end{equation}\begin{equation}\pdif{T}{t} +v \nabla T = \chi \Delta T,\label{eq:in:t}\end{equation}\begin{equation}\pdif{c}{t} + v\nabla c = D \nabla\left( \nabla c +\left( \frac{1}{l}\vec n_g+S_T \nabla T \right)c\right),\label{eq:in:3}\end{equation}

Введем безразмерные переменные выбрав в качестве масштабов: $h$-- высота слоя$h^2/\chi$ -- времени,$\chi/h$ -- скорости,$\delta \theta$ -- температуры,$\rho \chi^2/h^2$-- давления,$\bar C$ -- концентрации. В безразмерных переменных система уравнений примет вид.\begin{equation}\pdif{v}{t} +v \nabla v= - \nabla p + P \Delta v + \vec n_g P\left( R T+ R_C C \right)\label{eq:in:v2}\end{equation}\begin{equation}\pdif{T}{t} +v \nabla T = \Delta T\label{eq:in:t2}\end{equation}\begin{equation}\pdif{c}{t} + v\nabla c = Le\nabla\left( \nabla c +\frac{1}{l}\left( \vec n_g+\frac{\varepsilon R}{R_C} \nabla T \right)c\right)\label{eq:in:32}\end{equation}

где введены следующие безразмерные параметры:\begin{equation}R=\frac{g\beta_T\delta T h^3}{\nu \chi}; \, R_c=\frac{g\beta_C \bar C h^3}{\nu \chi} \, \label{}\end{equation}\begin{equation}P=\frac{\nu}{\chi};\,\varepsilon = S_T \bar C\frac{\beta_C}{\beta_T};\,Le=\frac{D}{\chi}\label{}\end{equation}Нелинейная система (\ref{eq:in:v2})-(\ref{eq:in:v2}) решалась методами конечных разностей. Малость числа Льюиса приводит к необходимости использования довольно подробных сеток, ввиду того что может образовываться токая спиральная структура в распределении концентрации. основные расчеты производились на сетке 129х65.

Результаты численного моделирования

В случае когда $l \sim 1$ были обнаружены новые конвективные режимы, существование которых в каналах малой высоты $h<<l_{sed}$ по видимому не возможно.

Случай $l <<1$ рассматривался ранее в работах [5-7]. Напомним, что в данном случае конвекция начинается с образования стоячей волны которая потом переходит в бегущую волну. Вблизи порога наблюдается устойчивое течение в виде слабой стоячей волны.

При больших надкритичностях (большое число Релея). Стоячая волна увеличивается в интенсивности, при этом частота колебаний уменьшается. Начинается существенное перемешивание коллоида, что не наблюдается в слабой волне. Затем данное состояние теряет устойчивости система переходит в режим стационарной однородной конвекции. Не смотря на сильное течение в жидкости происходит разделение смеси под действием термодиффузии и седиментации, приводящее к потере устойчивости стационарного течения и о образованию бегущей волны.

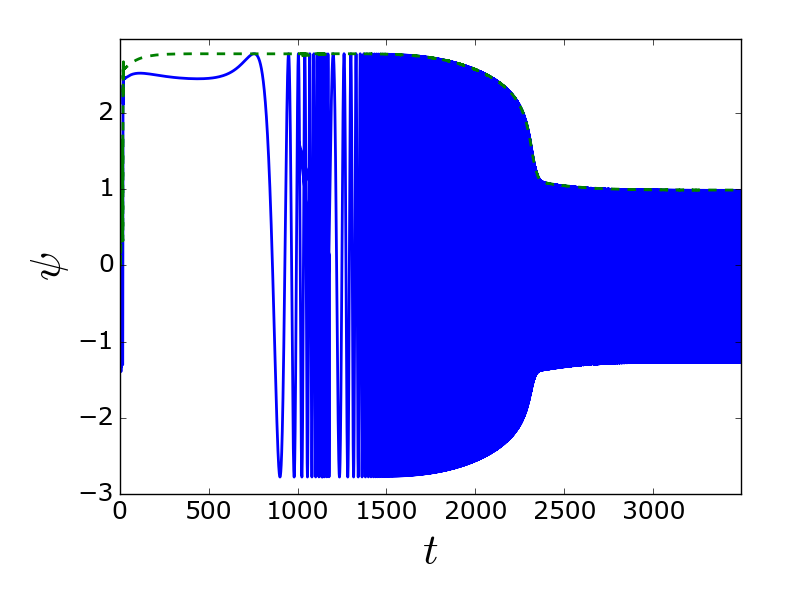
Анимация данного процесса приведена на видео 1. Эволюция течения занимает практически $3 \cdot 10^3$ единиц теплового времени. Поведение функции тока отображено на рис. 3 .

Работа выполнена при поддержке гранта 16-31-60074 .