\(\def\vec#1{\boldsymbol #1}\)

\(\def\pdif#1#2{\frac{\partial #1}{\partial #2}}\)\(\def\e{\mathrm{e}}\)\(\def\diff{\mathrm{d}}\)

Введение

Дисперсные системы, состоящие из компонентов разной плотности подвержены гравитационному разделению, когда под действием силы тяжести концентрация тяжелой компоненты становиться выше в нижних слоях жидкой дисперсионной фазы. В молекулярных растворах данный эффект проявляется слабо, и существенная неоднородность концентрации может наблюдаться только при очень больших вертикальных размерах системы.

В коллоидных системах, состоящих из жидкости носителя и наноразмерной примеситвердых частиц, эффект гравитационного разделения проявляется при сравнительномалой высоте. Так, в экспериментах по исследованию конвективных теченийколлоидных смесей, обнаружено влияние гравитационной стратификации смеси дажепри размерах полости в несколько миллиметров[5,6,7,8,9].

В слабоконцентрированных растворах полагается, что поток частиц, обусловленный полем тяжести, пропорционален концентрации и обратно пропорционален седиментационной длине:\begin{equation} j_{\mathrm{s}} = \frac{D}{l} \varphi. \label{eq:j_sed}\end{equation}Здесь $D$ --- коэффициент диффузии, $l$ --- длина седиментации, характеризующаявысоту, на которой концентрация примеси изменяется в $\e$ раз и определяемаясоотношением [10]:\begin{equation} l = \frac{k_{\mathrm{B}} T}{m_* g},\end{equation}где $k_{\mathrm{B}}$ --- постоянная Больцмана, $T$ --- температура, $m_* = v_{\mathrm{p}} ( \rho_{\mathrm{p}} - \rho_{\mathrm{s}} )$ --- эффективная масса наночастицы в жидкости носителе, $v_{\mathrm{p}}$ --- объем наночастицы, $\rho_{\mathrm{p}}$, $\rho_{\mathrm{s}}$ --- плотность наночастиц и жидкости носителя соответственно.

Диффузионный поток в приближении малых концентраций определяется классическим законом Фика, который в одномерном случае имеет вид\begin{equation} j_{\mathrm{d}} = - D \pdif{\varphi}{z}. \label{eq:j_diff}\end{equation}В этом случае решение уравнения сохранения для концентрации\begin{equation} \pdif{\varphi}{t} + \pdif{}{z} \bigl( j_{\mathrm{s}} + j_{\mathrm{d}} \bigr) = 0\end{equation}приводит к экспоненциальному барометрическому распределению частиц по высоте.Кинетика процесса седиментации частиц в данном приближении подробно рассмотренав [11].

В концентрированных коллоидных растворах формулы для потоков (\ref{eq:j_sed}),(\ref{eq:j_diff}) перестают быть справедливыми. В работе[12] это экспериментально и теоретически показано на примеремагнитной жидкости в гравитационных и магнитных полях. При этом использоваласьзависимость коэффициента диффузии от локальной концентрации примеси, полученнаяв классической работе [1] в приближении отсутствия взаимодействия твердых частиц с жидкой матрицей.Однако уравнение диффузии [12] довольногромоздкое и не имеет аналитического решения, что затрудняет теоретическийанализ состояния механического равновесия.В тоже время границы применимости более простых выражений для потоков (\ref{eq:j_sed}),(\ref{eq:j_diff}) являются довольно размытыми.

Благодаря простойфункции энергии межчастичного взаимодействия газ твердых сфер имеет несколько теоретических моделейразной степени сложности и достоверности с известными уравнениями состояния[13]. С теоретической точки зрения интерес представляет определение границ применимости различных приближений: вириальное разложение, уравнение Вертхейма--Тьеля (в приближении Перкуса--Йевика) и уравнение Карнагана--Старлинга.Так, например, в задачах линейного анализа устойчивости состояния механического равновесия системы необходимо знать начальное распределение наночастиц. Использование более простых приближений, имеющих аналитические решения, может значительно упростить исследование свойств стратифицированных сред.

Математическая модель

Рассмотрим равновесное распределение сферических частиц массой $m$ при учете гравитационной стратификации.Пусть замкнутый сосуд с вертикальными стенками высотой $h$ заполненгазом твердых сфер. Газ находится в поле тяжести $\mathbf g$ и поддерживается припостоянной температуре $T$. Ось $Z$ направлена вертикально вверх, против силы тяжести.

В случае идеального газа, уравнение состояния имеет вид:\begin{equation} P = n k_{\mathrm{B}} T,\end{equation}где $P$ --- давление газа, $n$ --- число молекул газа в единице объема. С другой стороны, приращение давления, создаваемоесобственным весом газа (гидростатическое давление), описывается выражением:\begin{equation} \diff P = - n m g \diff z,\end{equation}которое совместно с уравнением состояния дает дифференциальное уравнение, описывающее распределение частиц по высоте: \begin{equation} \diff n/n = - \diff z/l. \label{eq:ideal}\end{equation}Решая уравнение (\ref{eq:ideal}) с учетом условия постоянства среднего числа частиц в системе:\begin{equation} \frac{1}{h} \int\limits_0^h n \diff z = \bar n,\end{equation}где $\bar n $ --- средняя концентрация частиц в объеме, получим хорошо известное барометрическое распределение:\begin{equation} n_{\text{ид}} = \frac{\bar n h}{l}\frac{\e^{-z/l}}{1 - \e^{-h/l}}. \label{eq:dist_ideal}\end{equation}

Рассмотрим, как изменится данное распределение при учете конечного размерачастиц. Уравнение состояния слабонеидеального газа в виде вириального разложенияс точностью до второго коэффициента в приближении твердых сфер имеет вид[13]:\begin{equation} P = n k_{\mathrm{B}} T ( 1 + 4 v_{\mathrm{p}} n ),\end{equation}Следуя выводу уравнения \eqref{eq:ideal}, получим:\begin{equation} ( 1 + 8 n v_{\mathrm{p}} ) \frac{\diff n}{n} = - \frac{\diff z}{l}. \label{eq:virial}\end{equation}Для удобства сопоставления результатов разных моделей перейдем от числовой концентрации частиц к их относительной доле ---\begin{equation} \eta = \frac{n}{\bar n} = \frac{\varphi}{\bar \varphi}, \end{equation}где $ \bar \varphi $ --- среднее значение объемной доли примеси. С учетом связи$\varphi = n v_{\mathrm{p}} $ уравнение (\ref{eq:virial}) примет вид:\begin{equation} ( 1 + 8 \eta \bar \varphi ) \frac{\diff \eta}{\diff z}+\frac{\eta}{l} = 0. \label{eq:eta_virial}\end{equation}Данное дифференциальное уравнение имеет точное решение в виде функции Ламберта[14]:\begin{equation} \eta = \frac{1}{8 \bar{\varphi}} W \left( 8 \bar \varphi A \e^{-z/l} \right). \label{eq:dist_virial}\end{equation}Константа $A$ находится из условия сохранения общего количества частиц:\begin{equation} \frac{1}{h} \int \limits_0^h \eta \diff z = 1. \label{eq:eta_cond}\end{equation}

Интегрирование \eqref{eq:eta_cond} приводит к трансцендентному уравнению относительно константы $A$, поэтому для его решения воспользуемся условием малости $\bar \varphi$ (при больших значениях данного параметра в вириальном разложении необходимо учитывать слагаемые следующих порядков). Найдем приближенное решение, сделав подстановку \eqref{eq:dist_virial} в уравнение \eqref{eq:eta_cond} и производя разложение с точностью до слагаемых порядка $O(\bar \varphi^3)$:

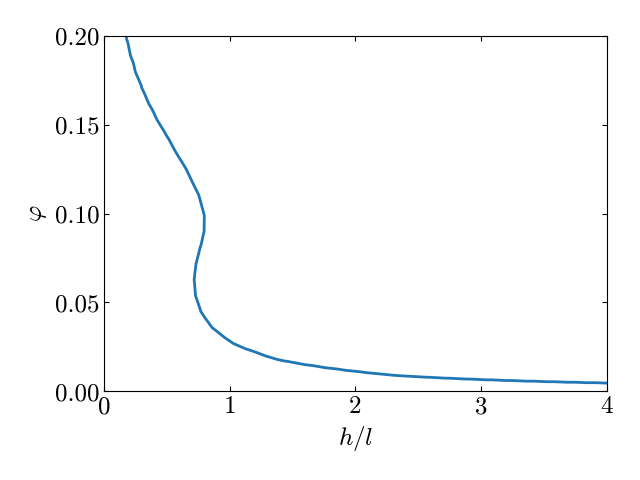
\begin{equation} \eta_{\text{вир}} \approx \eta_0 + 8 \left(\eta_0 \right)^2 \times \left( \frac{1+\e^{-h/l}}{2\e^{-z/l}}-1\right)\bar \varphi+\\+2^5\eta_0^3\left( \frac{1+\e^{-h/l}}{2\e^{-z/l}}-3-\e^{\frac{-h+2z}{l}}\right) \bar \varphi^2 .\end{equation} где введено обозначение\begin{equation}\eta_0= \frac{h}{l}\frac{\e^{-z/l}}{1-\e^{-h/l}}\end{equation} Полученное выражение позволяет вычислить среднеквадратичное отклонение $\varepsilon$ от барометрического распределения идеального газа ---\begin{equation}\varepsilon = \sqrt{\frac{1}{h}\int\limits_{0}^{h} \Bigl(\eta_{\text{вир}}-\eta_{\text{ид}} \Bigr)^2\diff z}.\label{eq:epsilon}\end{equation}Разрешая \eqref{eq:epsilon} относительно средней концентрации $\bar \varphi$, получим границу области применимости приближения идеального газа.Зависимость ${\bar \varphi_{\text{гр}}}$ при и $\varepsilon=0.05$ приведена на рис. 1 .При заданном $\varepsilon$ максимально допустимая средняя концентрация резко убывает с ростом $h/l$. При высоте сосуда порядка седиментационной длины $h/l=1$ модель барометрическое распределение справедливо если средняя концентрация меньше $\bar \varphi_c \approx 0.03$

Уравнение состояния газа твердых сфер, полученное Вертхеймом и Тьельем в приближении Перкуса--Йевика, описывается уравнением:\begin{equation} \frac{P}{n k_{\mathrm{B}} T} = \frac{1 + \bar \varphi \eta + ( \bar \varphi \eta)^2}{( 1 - \bar \varphi \eta )^3}, \label{eq:pe}\end{equation}а Карнагана--Старлинга, соответственно:\begin{equation} \frac{P}{n k_{\mathrm{B}} T} = \frac{ 1 + \bar \varphi \eta + ( \bar \varphi \eta )^2 - ( \bar \varphi \eta )^3 }{ ( 1 - \bar \varphi \eta )^3 }. \label{eq:ks}\end{equation}Производя аналогичную для вириального ряда процедуру, получим искомые дифференциальные уравнения концентрации частиц по высоте

--- для уравнения Вертхейма--Тьеля:\begin{equation} \frac{ ( 2 \bar \varphi \eta + 1 )^2 }{ ( 1 - \bar \varphi \eta )^4 } \frac{ \diff \eta }{ \diff z } + \frac{\eta}{l} = 0; \label{eq:diff_pe}\end{equation}

--- в приближении Карнагана--Старлинга:\begin{equation} \left( 1 + \frac{ 2 \bar \varphi \eta ( 4 - \bar \varphi )^2 }{ ( 1 - \bar \varphi \eta)^4 } \right) \frac{ \diff \eta }{ \diff z } + \frac{\eta}{l}=0. \label{eq:diff_ks}\end{equation}

Отметим, что уравнения распределения частиц газа твердых сфер, выведенные из условия равенства дифференциалов давлений, могут быть получены строгим образом для коллоидных растворов. Следуя логике[1] химический потенциал для частиц примеси в коллоидном растворе определяется конфигурационныминтегралом взаимодействия частиц в пустоте. Вычисливконфигурационный интеграл в соответствующих приближениях получаться уравненияаналогичные \eqref{eq:virial},\eqref{eq:diff_pe},\eqref{eq:diff_ks} . Подобный подход для приближенияКарнагана--Старлинга рассмотрен в [2]. Таким образом, если разложения[1] справедливы, то полученные результаты для газа твердых сфер применимы и кколлоидным растворам.

Данные уравнения не могут быть решены аналитически в общем виде, однако допускают численное решение.Численное решение производилось путем сведения стационарной задачи \eqref{eq:pe}, \eqref{eq:ks} к нестационарной и решение ее методом конечных разностей. Таким образом, задача нахождения распределения концентрации частиц сводилась к решению закона сохранения:\begin{equation} \pdif{\eta}{t}+\pdif{j}{z}=0 \label{eq:convers_law}\end{equation}с граничными условиями \begin{eqnarray} j (t, z = 0) = j (t, z = h) = 0,\end{eqnarray}где $j$ --- суммарный поток частиц, определяемы соответствующим приближением:\begin{eqnarray} && j_{\text{ПЕ}}= \frac{ ( 2 \bar \varphi \eta + 1 )^2 }{ ( 1 - \bar \varphi \eta )^4 } \pdif{\eta}{z} + \frac{\eta}{l}, \\ && j_{\text{КС}}=\left( 1 + \frac{ 2 \bar \varphi \eta ( 4 - \bar \varphi )^2 }{ ( 1 - \bar \varphi \eta)^4 } \right) \pdif{\eta}{z} + \frac{\eta}{l},\end{eqnarray}и начальным условием\begin{equation} \eta (t = 0 , z) = 1.\end{equation}

Данный подход позволяет избежать необходимости решения дополнительного уравнения по сохранения средней массы примеси \eqref{eq:eta_cond}, так как при решении нестационарной задачи \eqref{eq:convers_law} среднее значение примеси всегда сохраняется. Расчеты производились с пространственным шагом $h_z = h/200$. Алгоритм реализован на языке \texttt{Fortran} и скомпилирован в виде подключаемого модуля для языка \texttt{Python}. Данный подход позволил довольно гибко настраивать параметры расчета для разных моделей.

Барометрическое распределение слабонеидеального газа

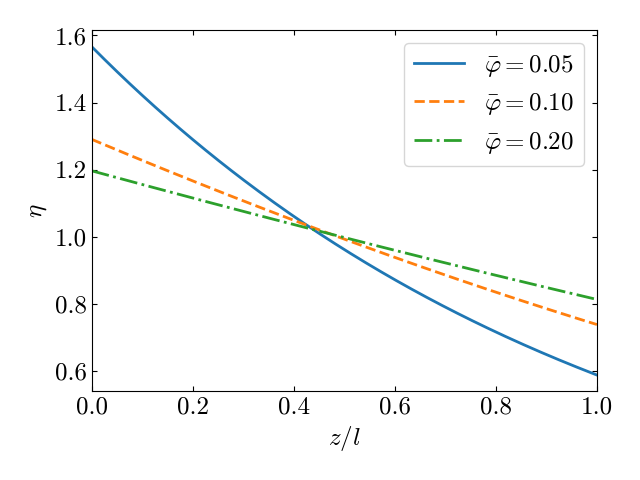
Сравним профили распределения частиц по высоте для идеального(\ref{eq:dist_ideal}) и слабонеидеального газа (\ref{eq:dist_virial}).В идеальном газе полагается, что частицы имеют нулевой объем, следовательнораспределение не зависит от объемной доли частиц. Учет размера частиц в линейном вириальном разложении приводит к существенному изменению профиля $\eta(z)$,даже при малой объемной доле частиц.Сравнение профилей распределения, описываемых выражением \eqref{eq:dist_virial} приразличных значениях объемной доли приведены на рис. 2

Стерическое взаимодействие молекул приводит к уменьшению градиента концентрации частиц. При значении седиментационной длины порядка высоты сосуда $l=h$, разность концентрации $\delta \eta = \eta(z=0)-\eta(z=1)$ для идеального и слабонеидеального отличаются почти в два раза при $\bar \varphi =0.1$ (рис. 2 ).

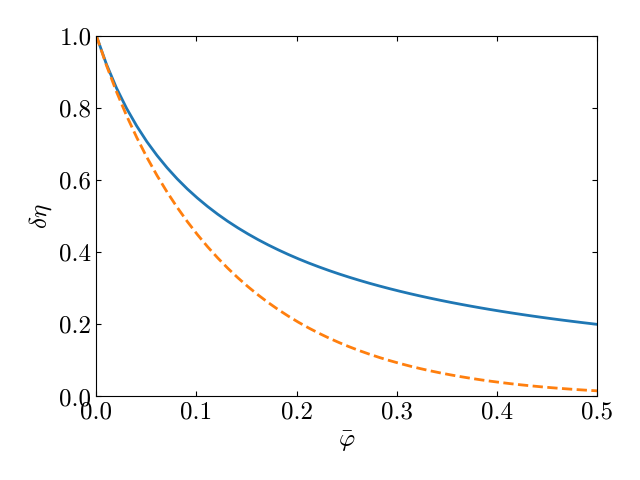
C увеличением объемной доли частиц характерная разность концентрации $\delta \eta$ уменьшается. Зависимость $\delta \eta (\bar \varphi)$ для уравнений \eqref{eq:eta_virial},\eqref{eq:pe} приведена на рис. 3 . Для идеального газа параметр $\delta \eta =1$ и не зависит от $\bar \varphi$.Численное решение уравнения в приближении Перкуса--Йевика \eqref{eq:diff_pe} отображено сплошной линией, вириальное разложение \eqref{eq:eta_virial} --- штриховой линией. При $\varphi>0.4$ $\delta \eta $ практически равно нулю. Отметим, что приближение Перкуса--Йевика и Карнагана--Старлинга имеют ограничения по объемной доле, и применимы в области $\varphi <0.47$ [13].

Значительные отклонения линейного вириального разложения от более точных моделей наблюдаются в области $\bar \varphi > 0.1$, что было вполне ожидаем. При $\bar \varphi =0.1$ значения параметра $\delta \eta $, полученное в линейном приближении, оказывается примерно на 20\% выше, чем в приближении Перекуса--Йевика.

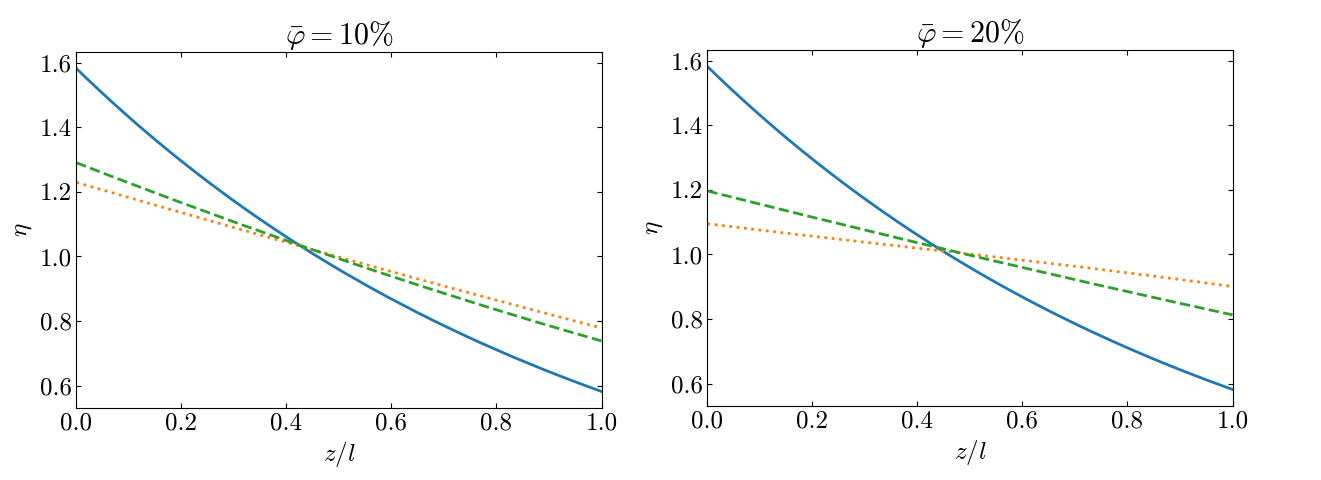
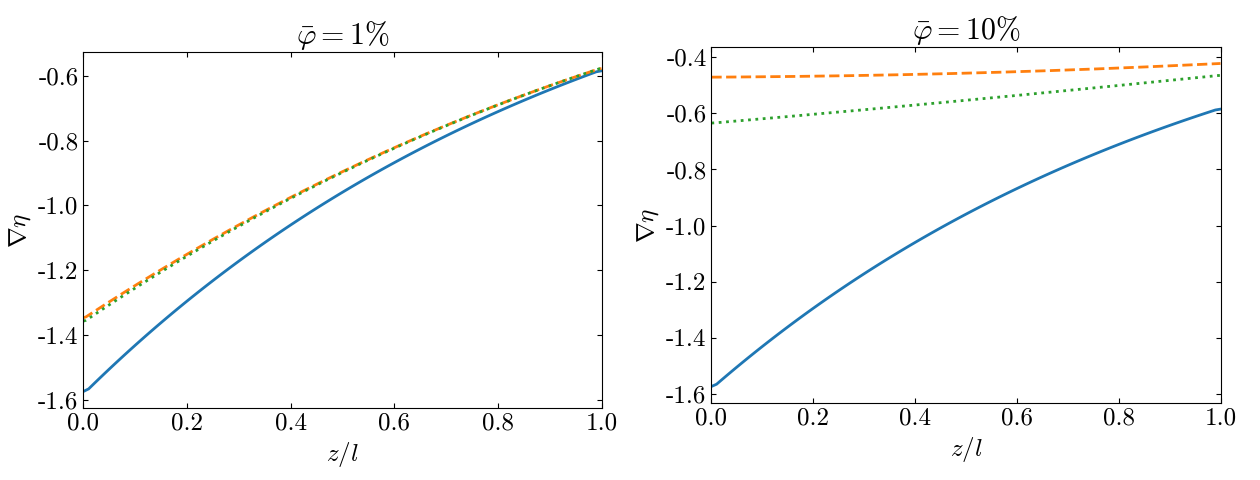
Профиль плотности числа частиц при различных значениях объемной доли приведены на рис. 4 . В области $\varphi =10\%$ распределения полученные в вириальном разложении и приближении Карнагана--Старлинга довольно близки, в то время как идеальный газ отличается значительно. Следовательно необходимым является учет стерического взаимодействия, однако можно ограничиться линейный вириальным разложением.

В задачах устойчивости состояния механического равновесия важным параметромявляется градиент концентрации, характеризующий градиент плотности. Зависимостьконцентрационного градиента от высоты для рассматриваемых приближений приведенына рис. 5 . При больших значения $\bar \varphi$ на нижнейгранице значение в приближении идеального и слабонеидеального газа отличаетсяболее чем в два раза.

Заключение

Проведен анализ распределения частиц газа твердых сфер в поле тяжести Земли. Для вириального разложения (с точностью до второго коэффициента) получено аналитическое уравнение распределение частиц (в приближении малой объемной концентрации). Проведено сравнение полученного уравнения с барометрическим распределением. Для модели идеального газа определена область применимости, в которой среднеквадратичное отклонение от более точной моделей мало.

В случае более сложных моделей газа твердых сфер в приближениях Перекуса--Йевика и Карнагана--Старлинга распределение частиц по высоте получены численным методом. Показано, что данные приближения дают практически одинаковый профиль объемной доли частиц. Существенные отклонения от вириального разложения наблюдаются только при $\varphi \gtrsim10\%$

На основе сравнения результатов разных моделей сделаны предположения о области применимости данных моделей. Так модель идеального газа применима при $\varphi\sim 3\%$, а модель вириального разложения при $\varphi\sim 8\%$. Исследования выполнены при финансовой поддержке Российского фонда фундаментальных исследований (№16-31-60074).

Работа выполнена при поддержке гранта 16-31-60074 .